21. Multiple Integrals in Curvilinear Coordinates
b. Integrating in Cylindrical Coordinates
3. Applications
Integrals in cylindrical coordinates are particularly useful when the integrand and/or the limits of integration are axially symmetric about the \(z\)-axis. We previously did Applications of Triple Integrals in rectangular coordinates. All of those applications can also be done using cylindrical coordinates.
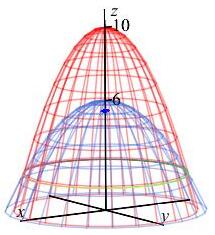
All the examples on this page of applications of triple integrals in cylindrical coordinates will use the solid between the paraboloids given by: \[ z=10-2x^2-2y^2 \quad \text{and} \quad z=6-x^2-y^2 \] as shown in the plot. Find the bounds on the integrals in cylindrical coordinates.
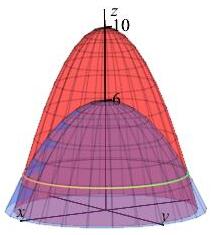
Both paraboloids opens downward. The first has its vertex at \((0,0,10)\). The second has its vertex at \((0,0,6)\). In cylindrical coordinates, the paraboloids are: \[ z=10-2r^2 \quad \text{and} \quad z=6-r^2 \] To find the intersection of the two paraboloids, we equate them: \[ 10-2r^2=6-r^2 \qquad \implies \qquad r^2=4 \] The solution is a circle of radius \(r=2\). So the bounds are \[ 0 \le \theta \le 2\pi \qquad 0 \le r \le 2 \qquad 6-r^2 \le z \le 10-r^2 \]
Volume
To find the volume of a 3D region \(R\) in cylindrical coordinates, the differential of volume \(dV\) must be expressed in cylindrical coordinates: \[ \text{Volume}=\iiint_R 1\,dV =\iiint_R r\,dr\,d\theta\,dz \]
Find the volume of the solid between the paraboloids.
Mass
To find the mass of a 3D region \(R\) in cylindrical coordinates, the density \(\delta\) must also be expressed in cylindrical coordinates: \[ M=\iiint_R \delta(x,y,z)\,dV =\iiint_R \delta(r,\theta,z)\,r\,dr\,d\theta\,dz \]
Find the mass of the solid between the paraboloids if its mass density is \(\delta=(x^2+y^2)z\).
Center of Mass
To find the center of mass of a 3D region \(R\) in cylindrical coordinates, the coordinates \(x\), \(y\) and \(z\) must also be expressed in cylindrical coordinates. So the center of mass is: \[ \bar{x}=\dfrac{M_x}{M} \quad \text{and} \quad \bar{y}=\dfrac{M_y}{M} \quad \text{and} \quad \bar{z}=\dfrac{M_z}{M} \] where the mass of the region is \[ M=\iiint_R \delta(x,y,z)\,dV =\iiint_R \delta(r,\theta,z)\,r\,dr\,d\theta\,dz \] and the \(x\), \(y\) and \(z\) \(1^\text{st}\)-moments of the mass, respectively, are \[\begin{aligned} M_x&=\iiint_R x\,\delta(x,y,z)\,dV =\iiint_R r\cos\theta\,\delta(r,\theta,z)\,r\,dr\,d\theta\,dz \\ M_y&=\iiint_R y\,\delta(x,y,z)\,dV =\iiint_R r\sin\theta\,\delta(r,\theta,z)\,r\,dr\,d\theta\,dz \\ M_z&=\iiint_R z\,\delta(x,y,z)\,dV =\iiint_R z\,\delta(r,\theta,z)\,r\,dr\,d\theta\,dz \end{aligned}\]
It is important to remember that we cannot compute \(\bar{r}=\dfrac{M_r}{M}\) and \(\bar{\theta}=\dfrac{M_\theta}{M}\) where \[\text{\Large\textcolor{red}Wrong}\qquad \begin{array}{rl} M_r&=\displaystyle\iiint_R r\,\delta(r,\theta,z)\,dV \\[8pt] M_\theta&=\displaystyle\iiint_R \theta\,\delta(r,\theta,z)\,dV \end{array} \qquad \text{\Large\textcolor{red}Wrong} \] because moments are only defined for rectangular coordinates since the balance beam derivation (\(\text{Torque} = \text{Force} \times \text{Lever Arm}\)) does not work for the \(r\) and \(\theta\) directions. If we want the cylindrical coordinates, \((\bar r,\bar\theta,\bar z)\) of the center of mass, we must first find the rectangular components and then convert to cylindrical.
Find the center of mass of the solid between the paraboloids if its mass density is \(\delta=(x^2+y^2)z\).
Centroid
The centroid of a region \(R\) in 3D is the same as the center of mass but with constant density which we take as \(\delta=1\). Then the mass reduces to the volume and the moments of mass become moments of volume. Thus the centroid is: \[ \bar{x}=\dfrac{V_x}{V} \quad \text{and} \quad \bar{y}=\dfrac{V_y}{V} \quad \text{and} \quad \bar{z}=\dfrac{V_z}{V} \] where \(V\) is the volume and the \(x\), \(y\) and \(z\) \(1^\text{st}\)-moments of the volume, respectively, are \[\begin{aligned} V_x&=\iiint_R x\,dV =\iiint_R r\cos\theta\,r\,dr\,d\theta\,dz \\ V_y&=\iiint_R y\,dV =\iiint_R r\sin\theta\,r\,dr\,d\theta\,dz \\ V_z&=\iiint_R z\,dV =\iiint_R z\,r\,dr\,d\theta\,dz \end{aligned}\]
Find the centroid of the solid between the paraboloids.
Average Value
To find the average value of a function over a 3D region in cylindrical coordinates, the function must be evaluated in cylindrical coordinates before integrating: \[ f_\text{ave}=\dfrac{1}{V}\iiint_R f(x,y,z)\,dV =\dfrac{1}{V}\iiint_R f(r,\theta,z)\,r\,dr\,d\theta\,dz \]
Compute the average of the temperature, \(T=x^2\), on the solid between the paraboloids.
4-Volume (Optional)
If \(f(x,y,z)\) and \(g(x,y,z)\) are functions on a region \(R\) in \(3\)-space and \(f(x,y,z) \ge g(x,y,z)\), then the 4-volume above the \(3\)-dimensional region \(R\) between \(w=g(x,y,z)\) and \(w=f(x,y,z)\) is: \[\begin{aligned} V_4&=\iiint_R f(x,y,z)-g(x,y,z)\,dV \\ &=\iiint_R (f(r,\theta,z)-g(r,\theta,z))\,r\,dr\,d\theta\,dz \end{aligned}\]
The base of a \(4\)-dimensional solid is the \(3\)-dimensional paraboloidal region discussed above. The upper surface is the graph of the function \(w=3z\). (Of course, the lower surface is \(w=0\).) Find the \(4\)-volume of this \(4\)-dimensional solid.
The exercises on the rest of this page refer to the ice cream cone below the paraboloid \(z=18-x^2-y^2\) above the cone \(z=3\sqrt{x^2+y^2}\). Find the limits of integration.
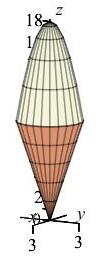
To find the \(r\) limits, find where the paraboloid hits the cone.
\(0 \le \theta \le 2\pi\)
\(0 \le \rule{0pt}{12pt}r \le 3\)
\(3r \le \rule{0pt}{12pt}z \le 18-r^2\)
Since the shape goes all the way around the \(z\) axis, the \(\theta\)
limits are \(0 \le \theta \le 2\pi\).
In cylindrical coordinates, the paraboloid is \(z=18-r^2\) and the cone is
\(z=3r\). So the \(z\) limits are given as \(3r \le z \le 12-r^2\).
To find the \(r\) limits, we equate the \(z\) equations:
\[\begin{aligned}
3r=18-r^2 \quad &\implies \quad r^2+3r-18=0 \\
\implies \quad (r+6)(r-3)=0 \quad &\implies \quad r = -6,3
\end{aligned}\]
Since \(r\) must be positive, the \(r\) limits are
\(0 \le r \le 3\).
Find the volume of the ice cream cone.
\(V=\dfrac{135\pi}{2}\)
We use the limits found in the previous problem: \[\begin{aligned} V&=\iiint_R dV=\int_0^{2\pi} \int_0^3 \int_{3r}^{18-r^2}\,r\,dz\,dr\,d\theta \\ &=\int_0^{2\pi} \int_0^3 (18-r^2-3r)r\,dr\,d\theta \\ &=2\pi \left[9r^2-\dfrac{r^4}{4}-r^3\right]_0^3 \\ &=2\pi \dfrac{135}{4} =\dfrac{135\pi}{2} \end{aligned}\] Note: The second line is the integral for the same volume but done using polar coordinates.
mj
Find the mass of the ice cream cone if the mass density is \(\delta=z\).
\(M=\dfrac{2673\pi}{4}\)
We use the limits found in a previous problem: \[\begin{aligned} M&=\iiint_R \delta\, dV =\int_0^{2\pi} \int_0^3 \int_{3r}^{18-r^2} z\,r\,dz\,dr\,d\theta \\ &=2\pi \int_0^3 \left[\dfrac{z^2}{2}\right]_{z=3r}^{z=18-r^2}\,r\,dr \\ &=\pi \int_0^3 ((18-r^2)^2-9r^2)\,r\,dr \\ &=\pi \int_0^3 \left(r^5-45r^3+324r\right)\,dr \\ &=\pi \left[\dfrac{r^6}{6}-\dfrac{45r^4}{4}+162r^2\right]_0^3 =\dfrac{2673\pi}{4} \end{aligned}\]
mj
Find the center of mass of the ice cream cone if the mass density is \(\delta=z\).
The density function and the object are both symmetric about the \(z\)-axis. What does this say about the \(x\)- and \(y\)-components of the center of mass?
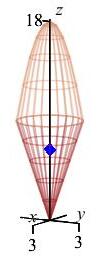
\((\bar x,\bar y,\bar z)=\left(0,0,\dfrac{603}{55}\right)\approx(0,0,10.96)\)
Since the shape and density are both symmetric about the \(z\)-axis, we conclude \(\bar x=\bar y=0\). We compute the \(z\)-moment of mass: \[\begin{aligned} M_z&=\iiint_R z\delta\, dV =\int_0^{2\pi} \int_0^3 \int_{3r}^{18-r^2} z^2\,r\, dz\, dr\, d\theta \\ &=2\pi \int_0^3 \left[\dfrac{z^3}{3}\right]_{z=3r}^{z=18-r^2}\,r\,dr =\dfrac{2\pi}{3} \int_0^3 \left((18-r^2)^3-27r^3\right)\,r\,dr \\ &=\dfrac{2\pi}{3} \int_0^3 \left(5832-972r^2+54r^4-r^6-27r^3\right)\,r\,dr \\ &=\dfrac{2\pi}{3} \int_0^3 \left(-r^7+54r^5-27r^4-972r^3+5832r\right)\,dr \\ &=\dfrac{2\pi}{3} \left[-\dfrac{r^8}{8}+9r^6-\dfrac{27r^5}{5}-243r^4+2916r^2\right]_0^3 \\ &=\dfrac{2\pi}{3} \dfrac{439587}{40} =\dfrac{146529\pi}{20} \end{aligned}\]
Since we previously computed \(M=\dfrac{2673\pi}{4}\), we conclude:
\[
\bar z=\dfrac{M_z}{M}=\dfrac{146529\pi}{20}\dfrac{4}{2673\pi}
=\dfrac{603}{55}\approx10.96
\]
Thus the center of mass is at:
\[
(\bar x,\bar y,\bar z)=\left(0,0,\dfrac{603}{55}\right)\approx(0,0,10.96)
\]
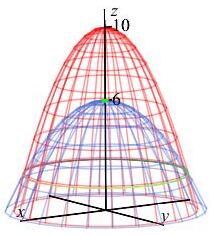
The center of mass is a blue diamond in the plot.
Notice the center of mass is above the center plane \(z=9\) since there
is more mass toward the top.
mj
Find the centroid of the ice cream cone.
The object is symmetric about the \(z\)-axis. What does this say about the \(x\)- and \(y\)-components of the centroid?
\((\bar x,\bar y,\bar z)=\left(0,0,\dfrac{99}{10}\right)=(0,0,9.9)\)
Again, the object is symmetric about the \(z\)-axis, so \(\bar x=\bar y=0\). We compute the \(z\)-moment of volume: \[ V_z=\iiint_R z\, dV=\int_0^{2\pi} \int_0^3 \int_{3r}^{18-r^2} z\,r\,dz\,dr\,d\theta \] This is the same integral as the mass. So \[ V_z=M=\dfrac{2673\pi}{4} \]
Since the volume is \(V=\dfrac{135\pi}{2}\), we conclude:
\[
\bar z=\dfrac{V_z}{V}=\dfrac{2673\pi}{4}\dfrac{2}{135\pi}=\dfrac{99}{10}=9.9
\]
Thus the centroid is located at:
\[
(\bar x,\bar y,\bar z)=\left(0,0,\dfrac{99}{10}\right)=(0,0,9.9)
\]
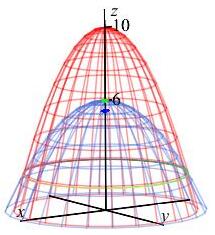
The centroid is a green sphere in the plot.
Notice the centroid is above the center plane \(z=9\) since there
is more volume toward the top.

mj
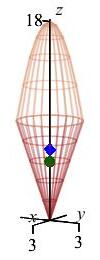
This plot shows the center of mass as well as the centroid.
The center of mass is plotted as a blue diamond.
The centroid at is plotted as a green sphere.
Notice that the center of mass is above the centroid because the
density, \(\delta=z\), is bigger toward the top.
Find the average value of the the function \(g(x,y,z)=y^2\) on the ice cream cone.
\(g_{\text{ave}}=\dfrac{36}{25}=1.44\)
In cylindrical coordinates, \(g(r,\theta,z)=y^2=r^2\sin^2\theta\). Thus: \[\begin{aligned} \iiint_R g\, dV&=\int_0^{2\pi} \int_0^3 \int_{3r}^{18-r^2} r^2\sin^2\theta\, r\, dz\, dr\, d\theta \\ &=\int_0^{2\pi} \int_0^3 (18-r^2-3r)\,r^3\sin^2\theta\, dr\, d\theta \\ &=\int_0^3 \left(18r^3-r^5-3r^4\right)\, dr \int_0^{2\pi}\dfrac{1-\cos(2\theta)}{2}\, d\theta \\ &=\left[\dfrac{9r^4}{2}-\dfrac{r^6}{6}-\dfrac{3r^5}{5}\right]_0^3 \left[\dfrac{\theta}{2}-\dfrac{\sin(2\theta)}{4}\right]_0^{2\pi} \\ &=\dfrac{486}{5}\pi \end{aligned}\] Finally, \[ g_{\text{ave}}=\dfrac{1}{V}\iiint_R g\, dV =\dfrac{2}{135\pi}\dfrac{486\pi}{5}=\dfrac{36}{25}=1.44 \]
mj
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum